Pertemuan 18 : Turunan Fungsi yang Memiliki 2 Variabel atau Lebih

April 29, 2020 motogokil Motorcycle 55

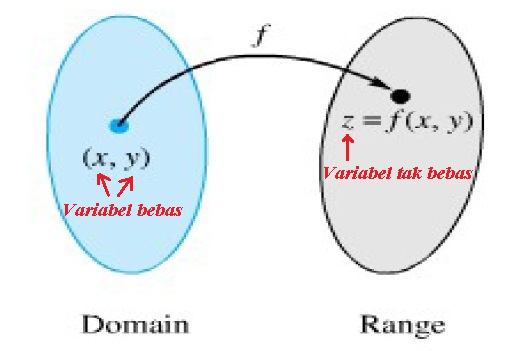
fungsi 2var

Pada pelajaran sebelumnya (matematika 1) sudah dipelajari fungsi dengan satu variabel bebas ( y = f(x) ). Pada bab 12 ini akan dipelajari fungsi yang memiliki 2 variabel bebas atau lebih yang dituliskan sebagai f(x,y) dan f(x,y,z). Seperti tampak pada gambar di atas, untuk sementara bab ini fokus pada fungsi dengan dua variabel bebas, baik daerah asal (domain) maupun daerah hasil (range) merupakan himpunan bilangan riil.

Contoh 1 :
Tentukan daerah asal alamiah dalam bidang-xy persamaan berikut
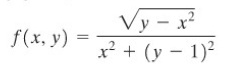
exp 1 prob

Jawab :
Daerah asal alamiah harus sedemikan rupa sehingga daerah asal yang dihasilkan dari fungsi di atas memenuhi persamaan himpunan bilang riil, yaitu :

  • Tidak bolah dibagi dengan 0
  • Tidak boleh ada akar negatif

Maka
exp 1 solv rev

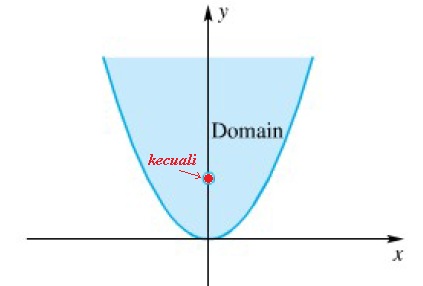
Gabungan dari pemenuhan dua syarat tersebut, maka daerah asal alamiah yang memenuhi adalah semua nilai (x,y) yang nilai y lebih besar atau sama dengan x², kecuali titik (0,1), yang digambarkan dalam grafik di bawah ini

exp 1 solv fig

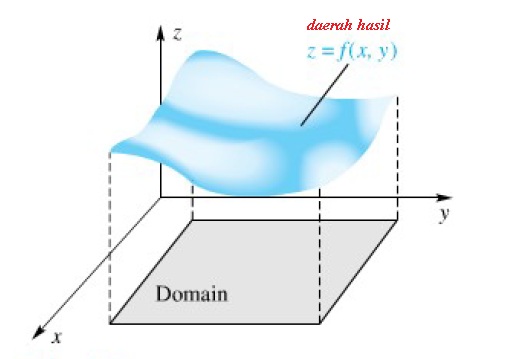
Posisi daerah asal dan daerah hasil pada fungsi dua variabel adalah seperti tergambarkan dalam grafik berikut

fungsi 2var domain n range

Contoh 2 :
Gambar fungsi dari
exp 2 prob

Jawab :
Karena z = f(x,y), maka agar didapatkan z dalam hinpunan bilangan riil maka

exp 2 solv

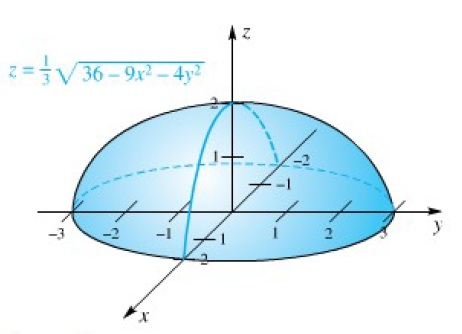
exp 2 solv fig

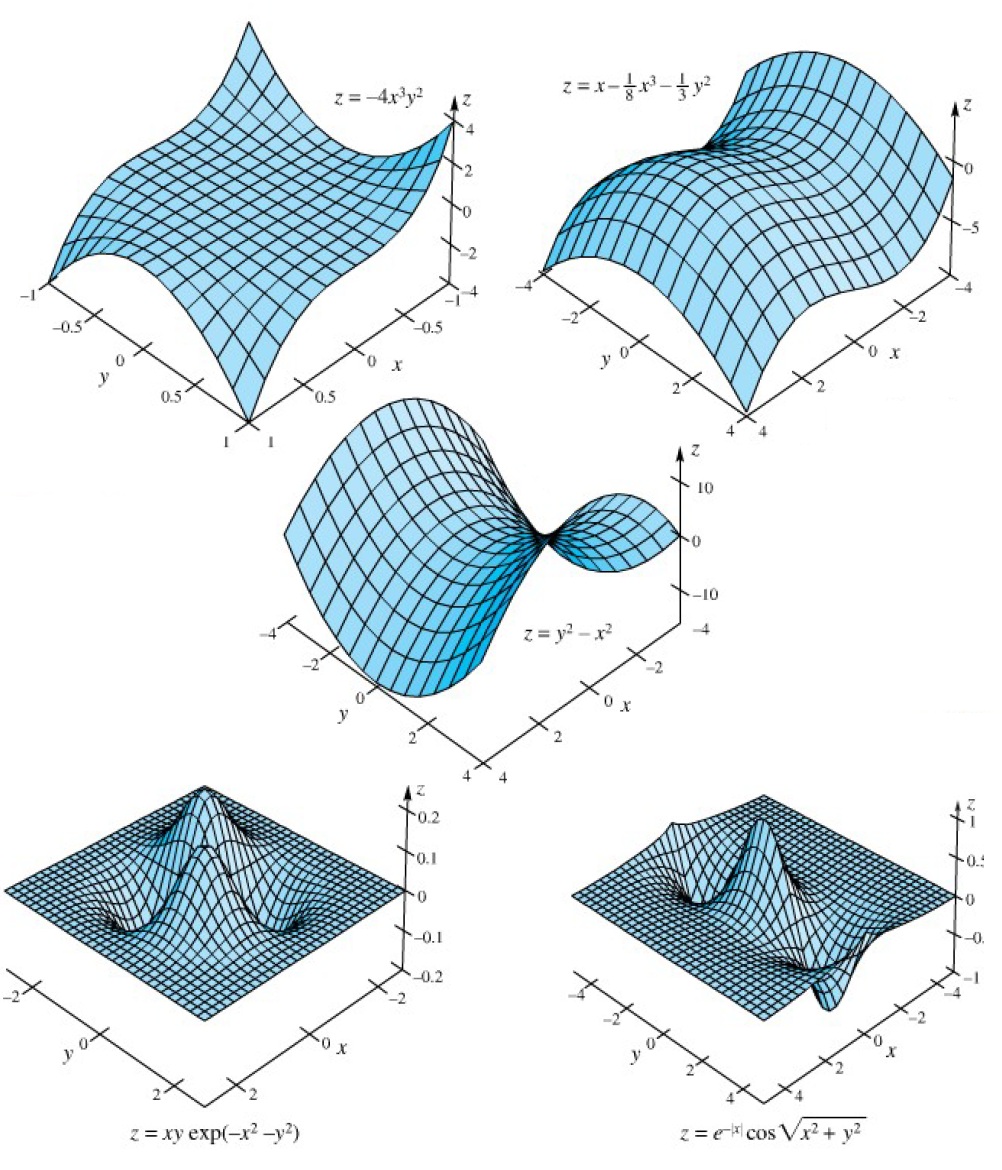
Fungsi seperti ini disebut sebagai fungsi permukaan, yang pernah dijelaskan di bab 11 yang lalu. Untuk fungsi-fungsi yang lain akan lebih mudah digambarkan dengan menggunakan pemrograman komputer. Berikut gambar-gambar fungsi permukaan yang digambarkan dengan menggunakan pemrograman komputer.

graph computerized

 

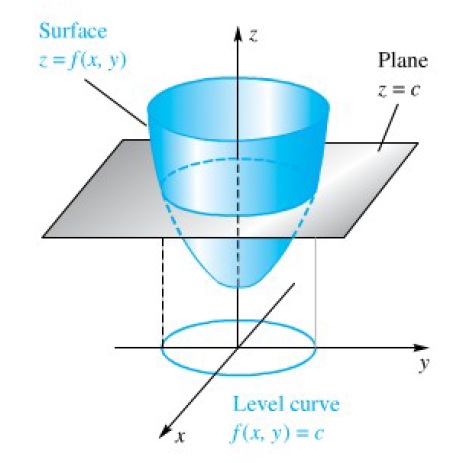
Kurva Ketinggian (level curve)

Teknik lain untuk menggambarkan fungsi 2 variabel adang denga kurva ketinggian (level curve). Kurva-kurva ini diperoleh dengan memotong permukaan fungsi dengan bidang datar (z=k).

level curve

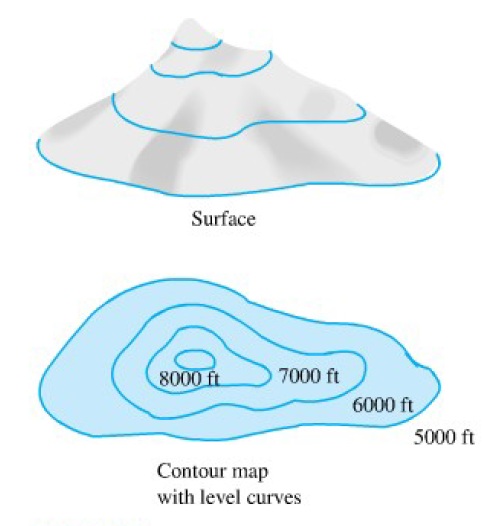
Kurva ketinggian juga disebut sebagai contour plot atau contour map. Sebagai contoh gambar kurva ketinggian dari sebuh bukit

contour map

Contoh 3 :
Buatlah kurva ketinggian dari
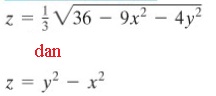
exp 3 prob

Jawab :
Untuk fungsi yang pertama bidang z yang digunakan sebagai pemotong posisinya lebih besar atau sama dengan 0, sampai nilai tertinggi yaitu ketikan x = y = 0, yaitu z =2 (tergambar sebagai sebuah titik di puncak elipsoid.

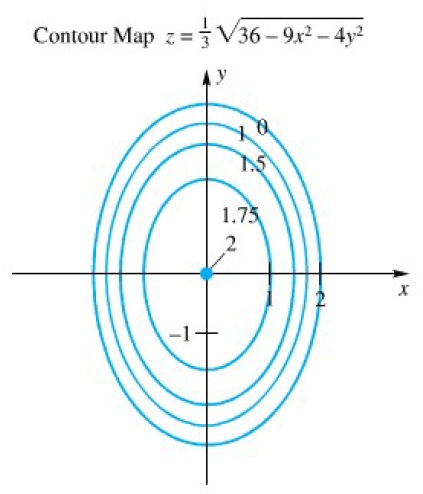
exp 3 solve fig

Sedangkan untuk fungsi yang ke-2 nilai untuk x dan y bisa positif, nol atau negatif
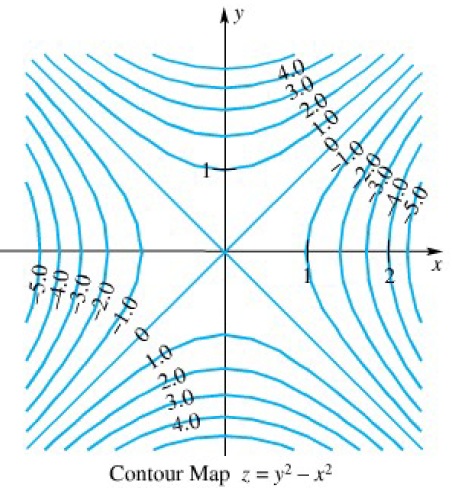
exp 3 solve fig2

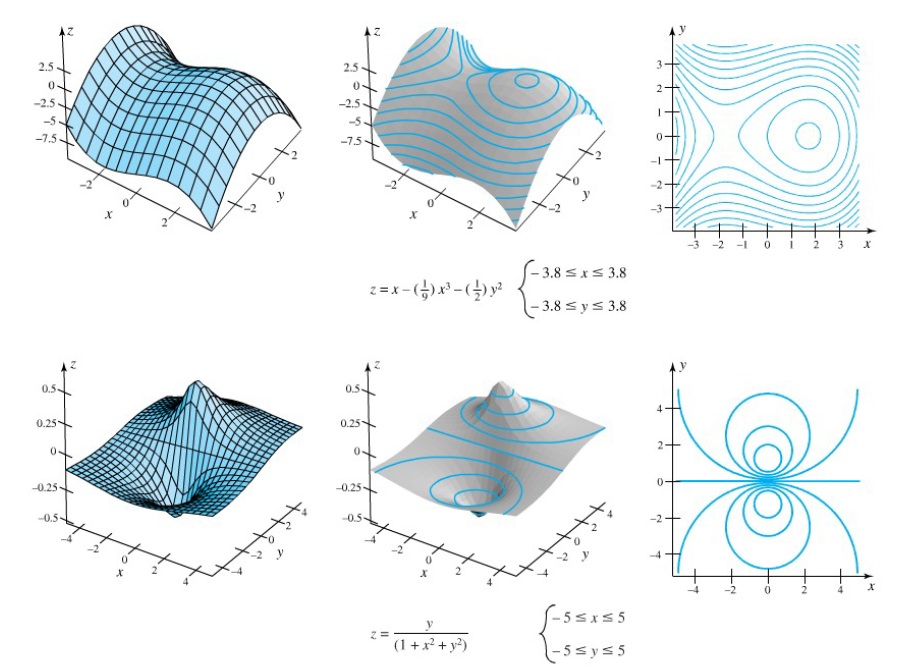
Penggambaran kurva ketinggian juga bisa dilakukan dengan pemrograman komputer. Dan jika dikombinasikan dengan gambar permukaan dengan menggunakan jaring-jaring (mesh) menjadi lebih mudah untuk difahami sebagai alternatif lain menggambar sebuah fungsi permukaan yang memiliki kontur (contour). Berikut ini beberapa gambar fungsi dengan kontur yang menarik, silahkan dicoba dengan menggunakan pemrograman komputer (matlab).

contour map plus1

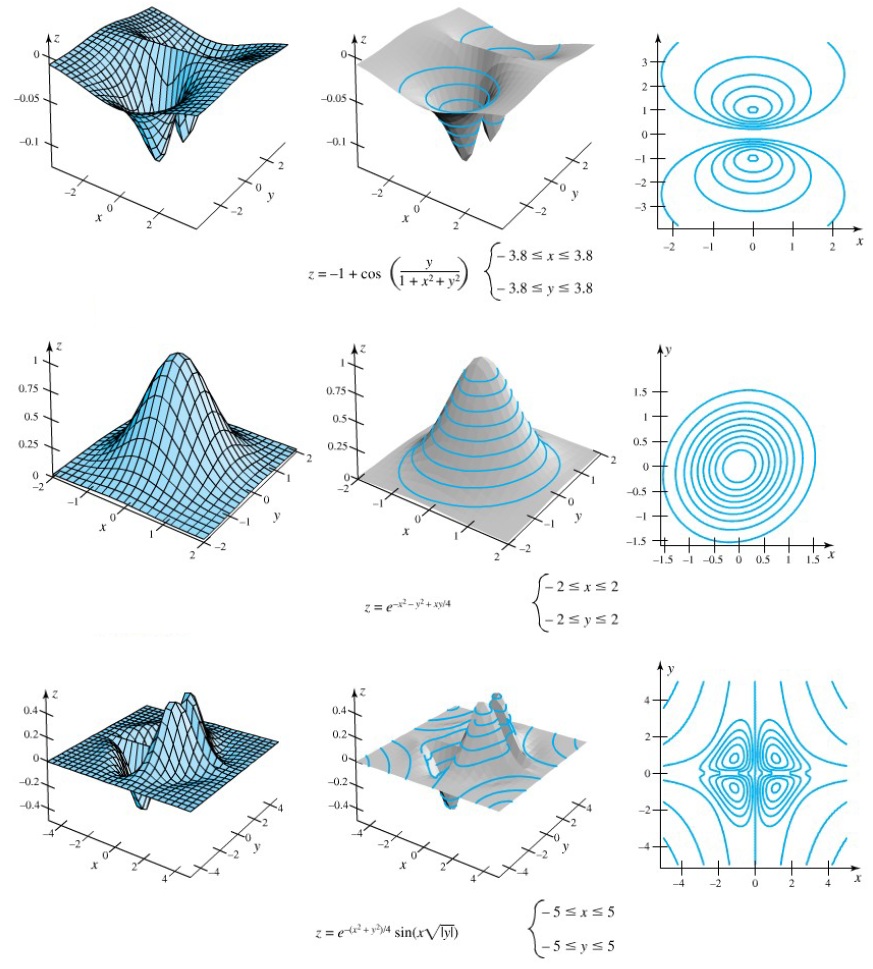
contour map plus2

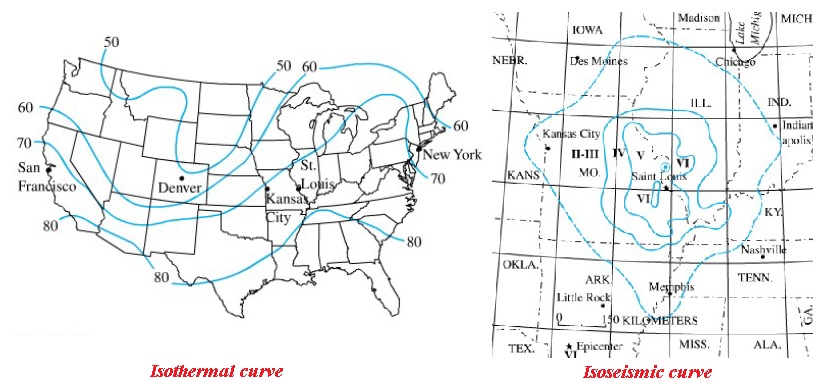
Aplikasi dari kurva ketinggian adalah penggambaran peta dengan adanya kurva dengan suatu nilai yang sama untuk paramater tertentu. Misalnya peta dengan garis isobar, artinya dalam peta tersebut tergambar kurva yang menghubungkan lokasi-lokasi dengan tekanan udara yang sama. Begitu pula dengan isoterm (suhu yang sama), isosiemic (intensitas gempa yang sama) dan sebagainya.

isothermal and isoseismic curve plot

 

Fungsi dengan 2 Variabel atau Lebih

Fungsi dengan 3 variabel atai lebih dapat digambarkan dengan menggunakan permukaan ketinggian.

Contoh 4 :
a. Tentukan daerah asal alamiah (domain) dari fungsi ini
exp 4 prob

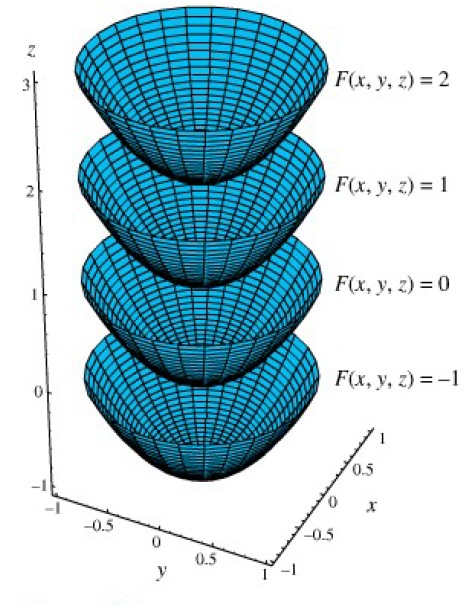
b. Dan gambar permukaan ketinggina adri fungsi berikut untuk ketinggian -1, 0, 1 dan 2.
exp 4 prob2

Jawab :
a. Daerah asal alamiahnya adalah mencari nilai (x, y, z) dimana
exp 4 solve1

b.
exp 4 solve2
exp 4 solve2 fig

Pertemuan Sebelumnya                                                   Pertemuan Selanjutnya

54 Komentar

1 Trackback / Pingback

  1. Pertemuan 19 : Turunan Parsial | the motorbike goes by skill or you get killed

Semoga tercerahkan dan komen mas bro juga ikut mencerahkan