Transformasi lapplace digunakan untuk memudahkan pemecahan persamaan diferensial dengan menggunakan aljabar biasa. Langkah-langkahnya adalah :
- Mentransformasilan persamaan diferensial kedalam bentuk lapplace (s) beserta dengan nilai awal dan nilai batasnya
- Memecahkan /memanipulasi persamaan “s” dengan aljabar
- Mnedapatkan solusi dengan meng invers lapplace kan persamaan “s”
Trnasformasi lapplace dapat dilakukan pada sebuah fungsi jika fungsi tersebut terdefinisi pada semua t yang sama dengan atau lebih besar dari 0. Dan teknik mentransformasikan ke dalam bentuk lapplace adalah dengan menggunakan integral sebagai berikut
Sedangkan untuk mendapatkan f(t) kembali adalah dengan transformasi invers lapplace
Beberapa contoh transformasi lapplace fungsi-funsi sederhana
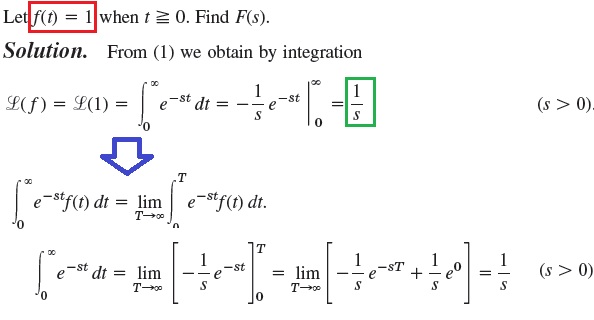
Contoh 1
Contoh 2
Sifat Linearitas Transformasi Lapplace
Aplikasi sifar linearitas lapplace
Contoh 1
Contoh 2
Lapplace untuk “t” pangkat “n”
Tabel lapplace beberapa fungsi dasar
Pergeseran Fungsi Lapplace “s” diganti dengan “(s-a)”
Pembuktiannya adalah persamaan ini
Contoh 1 : Pergeseran lapplace dari fungsi sin dan cos
Contoh 2 : Invers dari fungsi s yang tergeser
Penyelesaian : s² + 2s harus difahami sebagai bagian dari (s+1)² sehingga
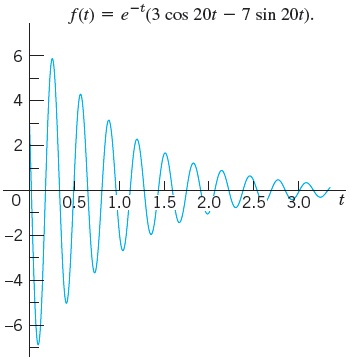
dan hasilnya adalah
Latihan : Kerjakan nomor 4,5,8,12 dan 43 dari soal berikut

Materi Sebelumnya Materi Selanjutnya


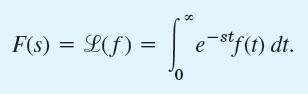
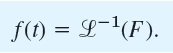

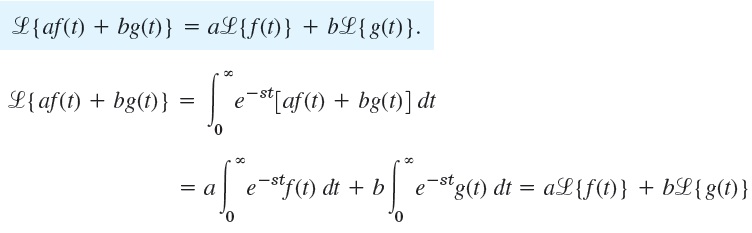
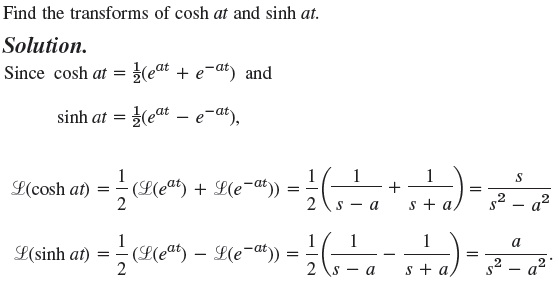

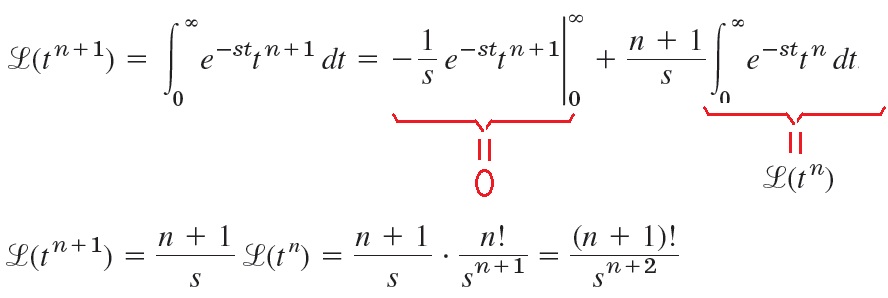


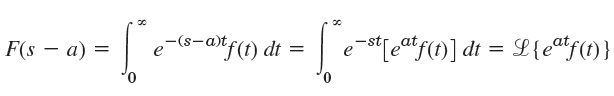
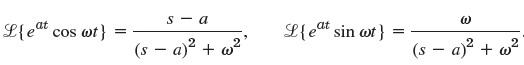
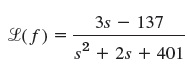
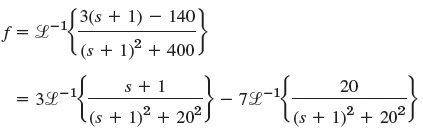
Kelas D