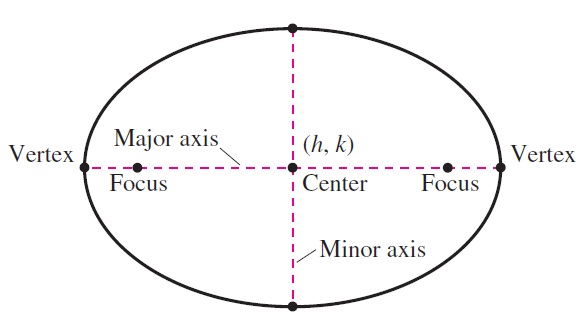
Elips (Ellips)
Elips memilki nilai eksentrisitas 0<e<1 ,memiliki 2 puncak (A dan A’) yang terletak pada sumbu mayornya.
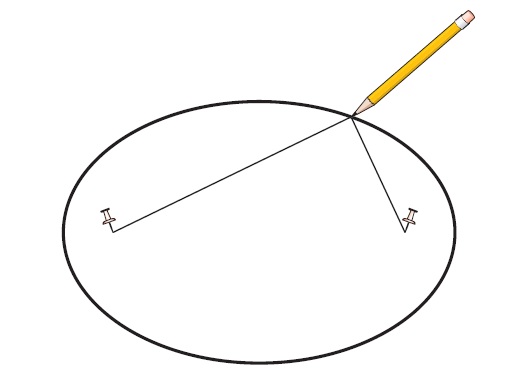
Untuk memudahkan membayangkan cara menggambar elips dan mentukan persamaannya adalah dengan gambar berikut
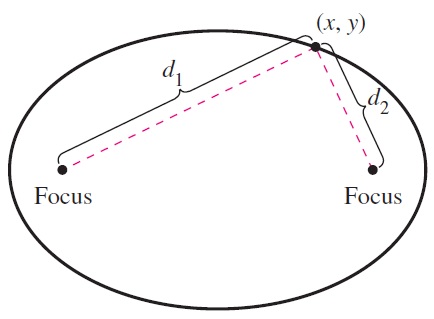
Pasang 2 buah paku pada jarak tertentu (jadikan sebagai fokus), ikatkan seutas benang yang panjangnya lebih besar dari jarak kedua pake tersebut. Kemudian buat gambar dengan pinsil pada kondisi di atas, dimana benang selalu dalam kondisi tegang (lurus). Jadi dapat disimpulkan bahwa elips adalah kumpulan titik yang jumlah jarak dengan kedua titik tetap (fokus) (d1 + d2) adalah sama.
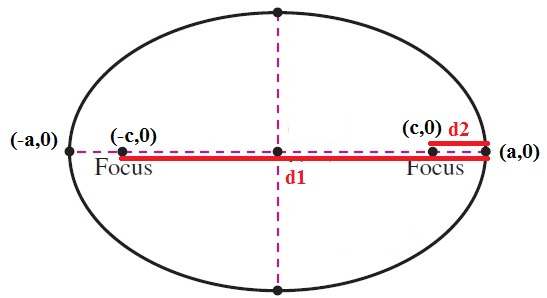
Sekarang mari kita tentukan persamaannya saat titik P (x,y) berada segaris dengan fokus-fokus nya
Maka jumlah panjang d1 + d2 adalah => (c + a) + (a – c) = 2a
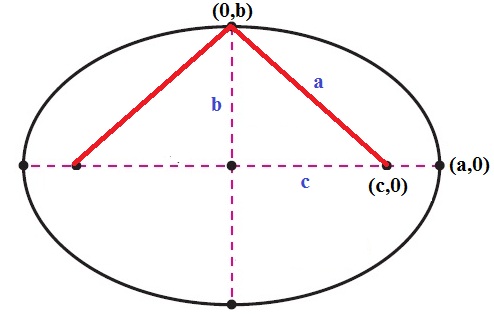
Maka persamaannya dapat dengan mudah diperoleh jika menggunakan titip P tepat di puncak sumbu minornya yaitu titik (0,b)
Jika c² + b² = a², maka penyederhanaan selanjutnya menghasilkan
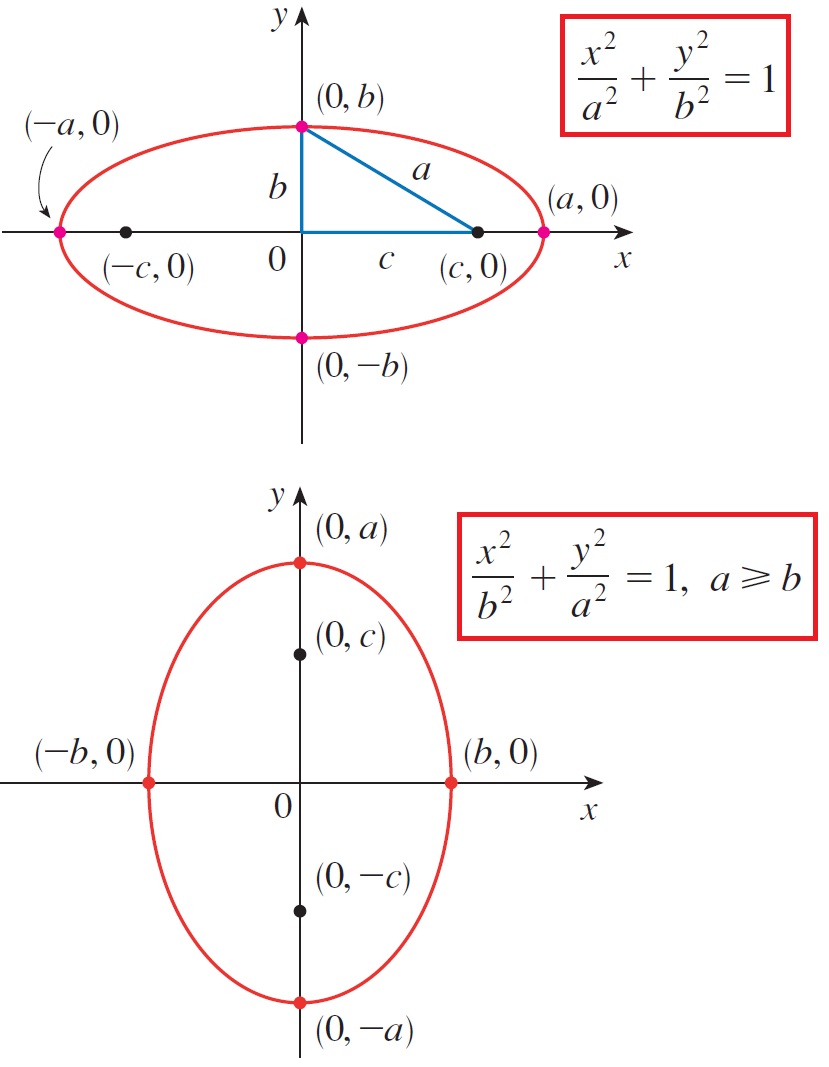
Jadi bentuk elip bisa dua macam, tergantung posisi sumbu mayor dan minornya
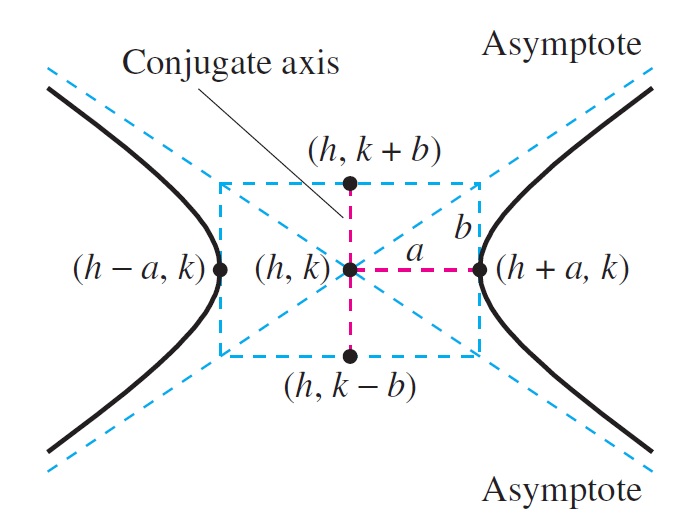
Hiperbola (Hyperbola)
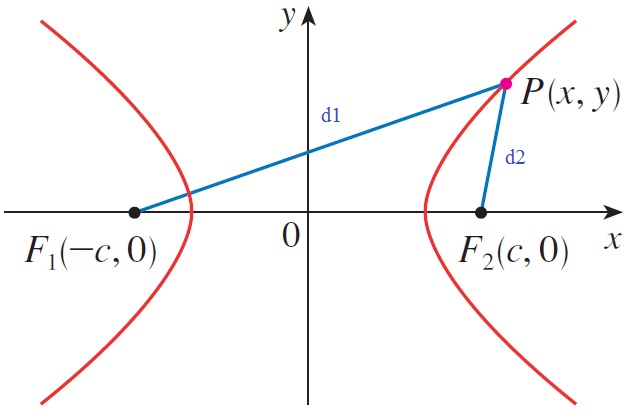
Untuk hiperbola mirip dengan elips, jika elip jumlah d1+d2 tetap, maka pada hiperbola selisih d1-d2 tetap
![]()
Sehingga persamaan yang nanti akan dihasilkan adalah
Hubungan antara a, b dan c dalam hiperbola
Kerjakan tugas dari sum bab 10.2 nomor : 16, 21, 25, 37 dan 51


Materi Sebelumnya Materi Selanjutnya


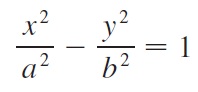
Leave a Reply