Pertemuan 10 : Fungsi dengan Periode 2L

Perubahan periode dari 2π menjadi 2L

Adalah bentuk fungsi yang lebih umum, ketimbang fungsi dengan periode 2π. Dan untuk mendapatkan bentuk deret fourier-nya harus dilakukan sedikit modifikasi, bagaimana merubah 2π = 2L. Berikut ini langkah-langkahnya

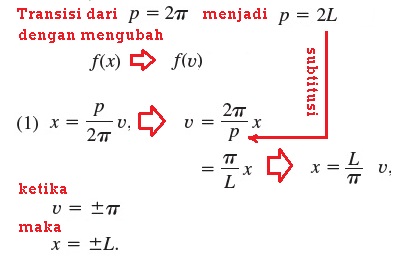
Perubahan di atas mengakibatkan perubahan deret fourier beserta koefisien-koefisiennya

Contoh 1 :
Carilah deret fourier dari fungsi berikut

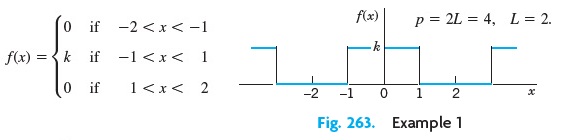
Jawab :

 

Contoh 2 :
Carilah deret fourier dari fungsi berikut

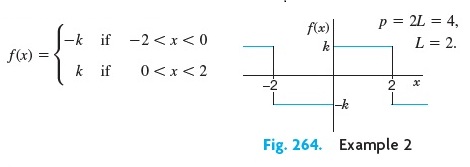
Jawab :

 

Contoh 3 :
Carilah fungsi penyearah setengah gelombang berikut ini

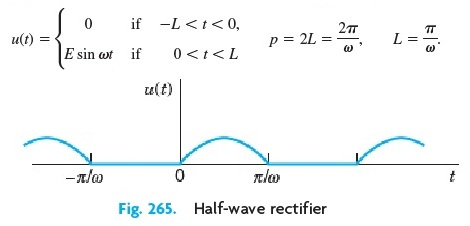
Jawab :

 

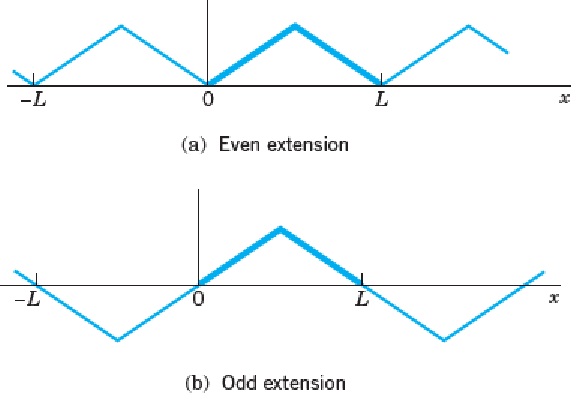
Penyederhanaan Fungsi Genap dan Ganjil

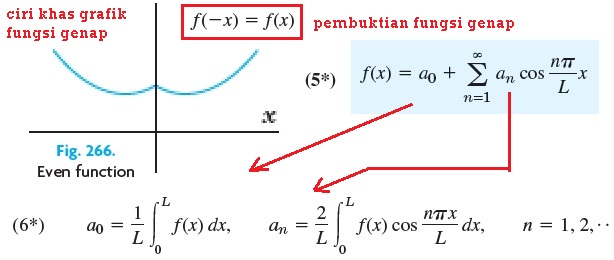
Jika fungsinya genap dengan pembuktian matematika f(-x) = f(x) , maka deret fourier tereduksi menjadi deret cosinus fourier

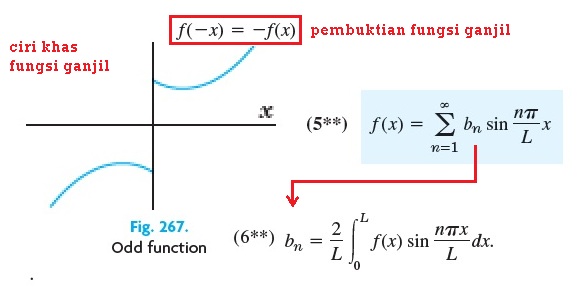
Sedangkan jika gungsi tersebut adalah fungsi ganjil dengan pembuktian matematika f(-x) = -f(x), maka persamaan deret fourier-nya tereduksi menjadi deret sinus fourier

Gunakan persamaan integral ini untuk menyederhanakan fungsi genap dan fungsi ganjil.

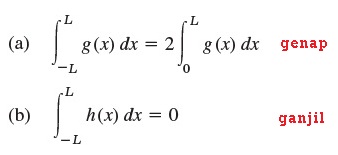
Contoh 4 :
Carilah deret fourier fungsi gigi gergaji berikut

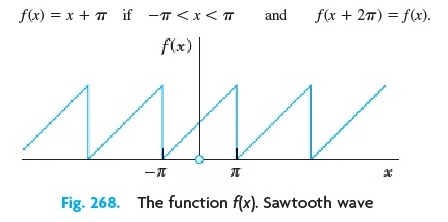
Jawab :
Jika melihat ciri khas dari gambar dan pembuktian matematika f(x) nya, maka fungsi seperti tidak bisa disederhakan sebagai fungsi genap dan fungsi ganjil. Akan tetapi jika dipecah menjadi dua fungsi sederhana, maka penyelesaiannya akan lebih mudah ketimbang haru mencari a0, an dan bn sekaligus.

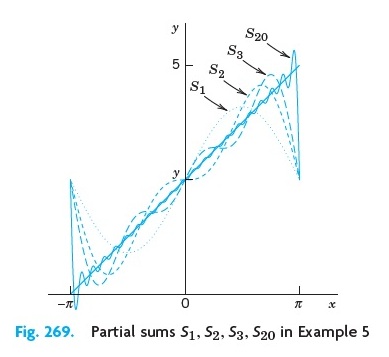
Gambar penjumlahan deret secara parsialnya ditunjukkan pada gambar di bawah ini. Dan semakin banyak suku yang ikut dijumlahkan dalam deret fourier, hasilnya akan semakin mendekati sinyal gigi gergaji

Perluasan Setengah Gelombang

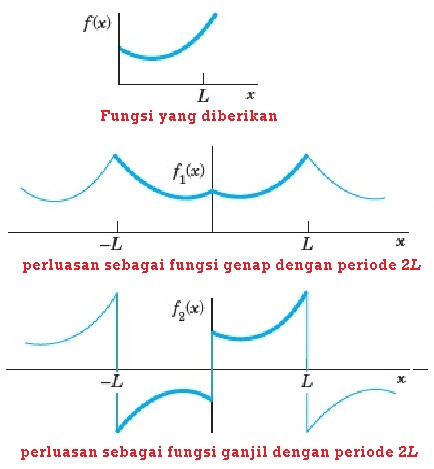
Adakalanya fungsi yang diberikan lebih umum lagi, yaitu hanya sepotong dan bukan merupakan fungsi periodik. Oleh karena itu untuk mendapatkan deret fourier-nya maka dilakukan perluasan sebagai fungsi genap dan fungsi ganjil.

Contoh 5 :
Carilah deret fourier dari perluasan fungsi genap dan fungsi ganjil dari fungi berikut

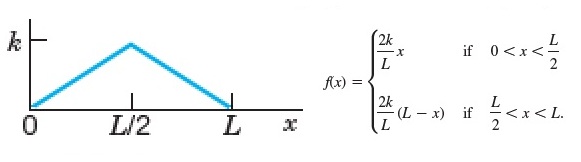
Jawab :
Fungsi yang hanya sepotong ini, kemudian diperluas menjadi fungsi genap dan fungsi ganjil dengan periode 2L. Yang gambar grafikanya sebagai berikut

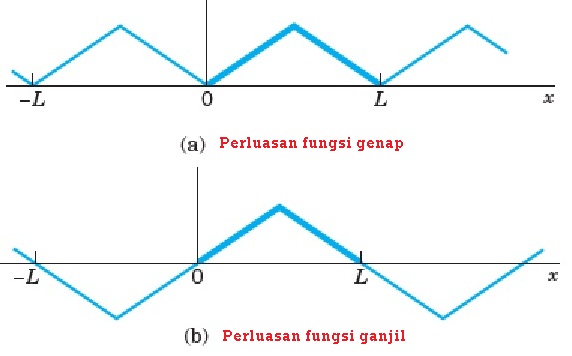
a. Deret fourier untuk perluasan genap

b. Deret fourier untuk perluasan ganjil

Latihan

Pertemuan Sebelumnya                                                Prtemuan Selanjutnya